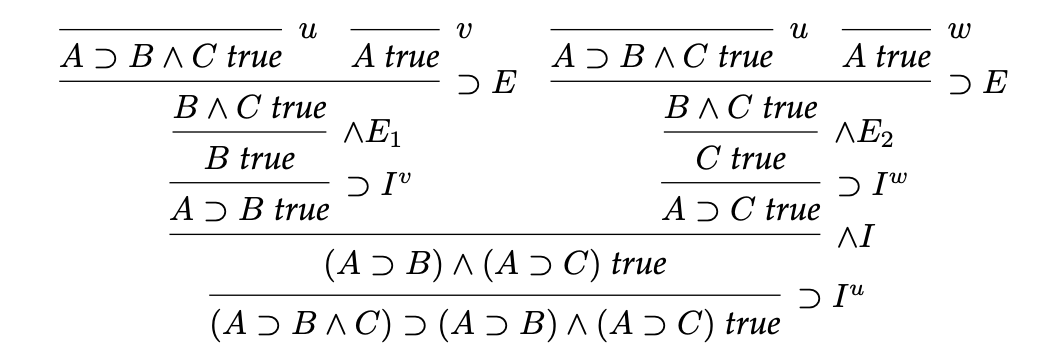lecture 02 Natural deduction

Table of contents

1. Some history

2. Inference rules

Constructive logic is all about proofs, which means that to decide if a judgment of the type A true holds, we need a proof of it.

conjunction

$A\wedge B$ has a proof iff A has a proof and B has a proof.

Note this defines the connectives in terms of proofs rather than truth value.

$\frac{A\, true \quad B\, true}{A\wedge B \, true}\wedge I$

The rule is named $\wedge I$, because it’s introducing the connective $\wedge$ between two props.

Elimination rules:

$\frac{A\wedge B \, true}{A\, true}\wedge E_1 \quad \frac{A\wedge B \, true}{B\, true}\wedge E_2$

Implication

$A \supset B$ has a proof iff the existence of a proof of A implies B has a proof.

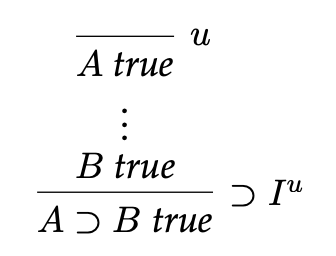
Note that the assumption $A \, true$ can only be used in this part of the proof.

elimination rule: $\frac{A\supset B \, true \quad A \, true}{B \, true}\supset E$

Truth

$\frac{}{\top \, true}\top I$

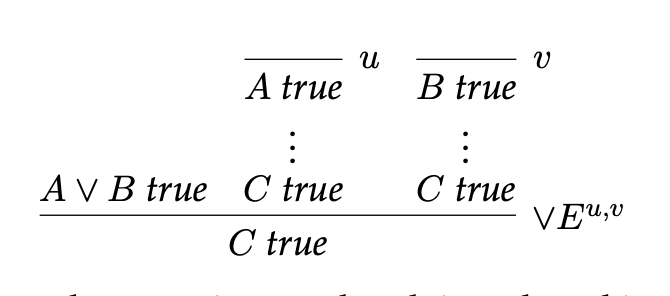
Disjunction

$A\vee B$ has a proof iff A has a proof or B has a proof.

Introduction rules:

$\frac{A\, true}{A \vee B \, true}\vee I_1 \quad \frac{B\, true}{A\vee B \, true}\vee I_2$

Elimination rule

Falsehood

$\frac{\bot \, true}{C \, true}\bot E$

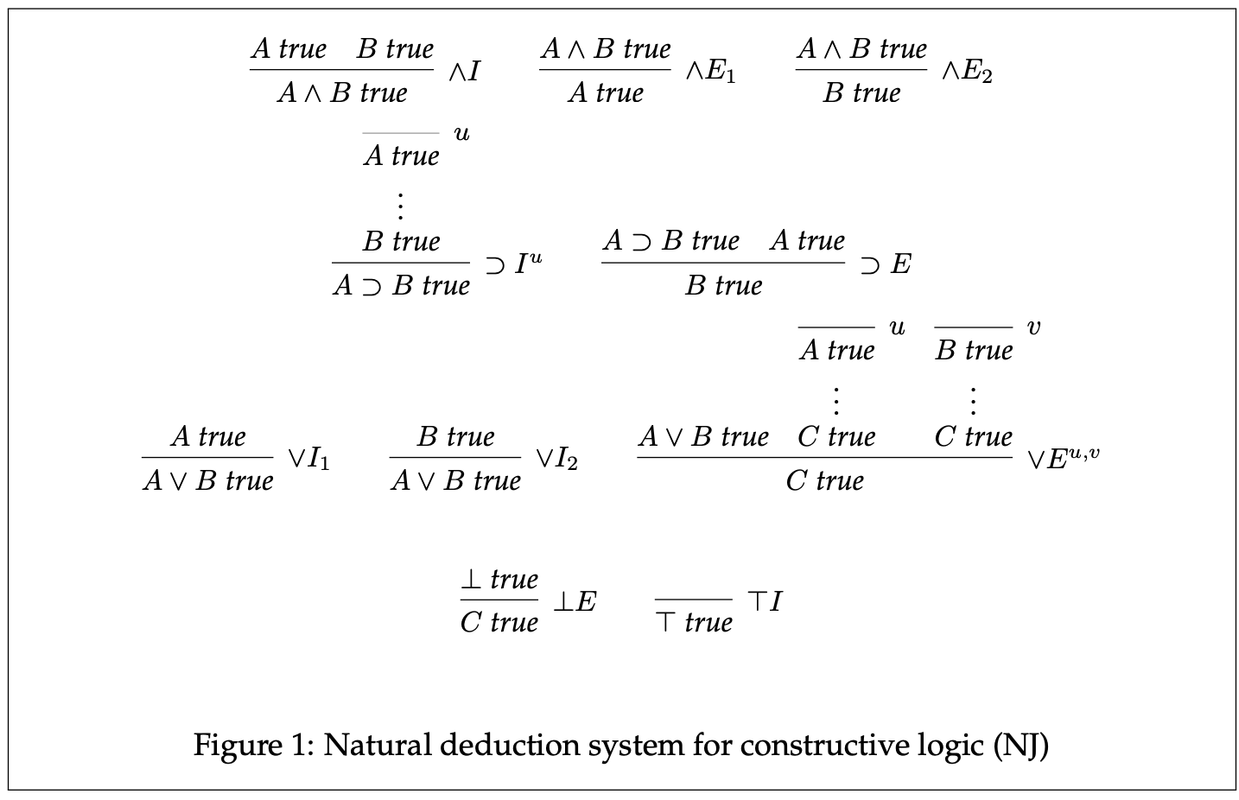
Summary

3. Proofs

Commutativity of conjunction

We can construct a proof of: $(A\wedge B) \supset (B\wedge A) \, true$

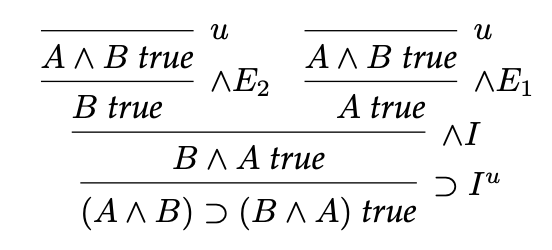
Commutativity of disjunction

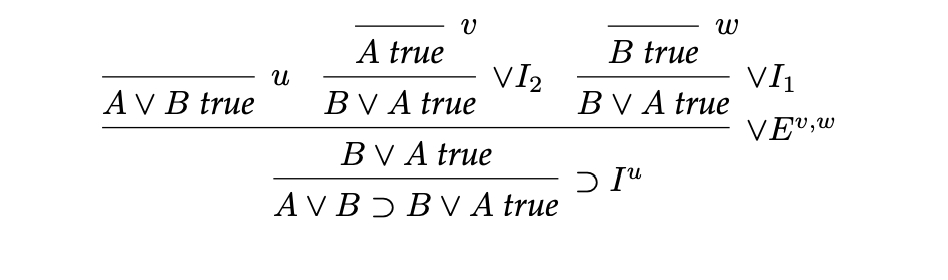
Distributivity of $\supset$ over $\wedge$