lec01. what’s constructive logic?

Table of contents

1. course overview

four main topics:

• proofs as evidence for truth.
• proofs as programs. relate logic and program via Curry-Howard isomorphism. we can interpret formulas as types, proofs of such formulas are actually programs of corresponding type.
• proof search as computation.
• advanced topics. linear logics, resolutino, theorem prover.

2. what’s logic

3. why anothor logic?

law of excluded middle: either $A$ or $\neg A$ holds.

Some theorems relies heavily on the law.

Constructive logic: the truth of a judgment is solely determined by an evidence of that judgment. It can be thought of as a proof-centered logic, and can be interpreted as algorithms.

4. First steps

Work with first-order logic.

• conjunction: $\wedge$
• disjunction: $\vee$
• implication: $\supset$
• false: $\bot$
• true: $\top$
• universal: $\forall$
• existential: $\exist$

We don’t use negation($\neg$), instead $\neg A$ can be written as $A\supset \bot$. We use upper case letters for formula variables. Lower case letters are reserved for predicate symbols and terms.

Defintion 1(Terms). The set of terms is inductively defined as follows:

• a variable is a term (x, y, z…)
• If f is a function symbol of arity n, then $f(t_1,...,t_n)$ is a term. In particular, if f has arity 0, it’s called constant.

Definition 2(Formulas). inductively:

• If p is a predicate symbol of arity n, then $p(t_1,...,t_n)$, for terms $t_1,...,t_n$ is a (atomic) formula.
• If A and B are formulas, then
  • $A\wedge B$
  • $A\vee B$
  • $A\supset B$
  • $\forall x.A(x)$
  • $\exist x.A(x)$

the precedence of logical operators:

$\wedge, \vee, \forall/\exist, \supset$

Consider the following formulas:

$\forall x.(even(x) \supset even(s(s(x))))$

Here, even is a predicate symbol, s is a function symbol. Both $x$ and $s(s(x))$ are terms.

• predicate symbol: combines terms and produces a predicate
• function symbol: combines terms and produces a new term.

In order to build proofs, we need to use a proof calculus. We’ll use natural deduction and sequent calculus, which use the same kind of building blocks: inference rules.

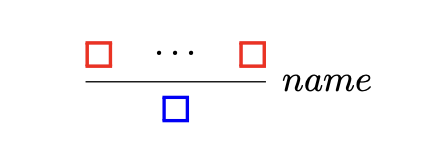red boxes are judgments for premises; blue box called conclusion.

A judgment is simply an assessment about an object.

An inference rule is interpreted as: if all the premises hold, then I can correctly conclude the conclusion.

Inference rules are presented with schema variables.

$\frac{N \, Nat \quad M \, Nat}{N + M \, Nat} +$

An inference rule can have zero premises, called axiom.

A proof is constructed by plugging in inference rules together, can be represented as a tree and a DAG.